Santa Cruz do Sul, 15 de agosto de 2008.
sexta-feira, 22 de agosto de 2008
Apresentação
Este blog foi desenvolvido pela acadêmica Patricia Andréia Schlittler, como atividade de pesquisa na disciplina de Informática Aplicada à Matemática, da Universidade de Santa Cruz do Sul - RS - Brasil.
Santa Cruz do Sul, 15 de agosto de 2008.
Santa Cruz do Sul, 15 de agosto de 2008.
A necessidade de contar e os diferentes recursos utilizados
Com o desenvolvimento das atividades humanas, surgiu, de acordo com http://pessoal.sercomtel.com.br/matematica/fundam/numeros/numeros.htm#m10101, a necessidade de contar. O homem começou a plantar, produzir alimentos, construir casas, proteções, fortificações e domesticar animais, usando os mesmos para obter a lã e o leite, tornando-se criador de animais domésticos, o que trouxe profundas modificações na vida humana.
A agricultura passou então a exigir o conhecimento do tempo, das estações do ano e das fases da Lua e assim começaram a surgir as primeiras formas de calendário.
A agricultura passou então a exigir o conhecimento do tempo, das estações do ano e das fases da Lua e assim começaram a surgir as primeiras formas de calendário.
No pastoreio, o pastor usava várias formas para controlar o seu rebanho. Pela manhã, ele soltava os seus carneiros e analisava ao final da tarde, se algum tinha sido roubado, fugido, se perdido do rebanho ou se havia sido acrescentado um novo carneiro ao rebanho. Assim eles tinham a correspondência um a um, onde cada carneiro correspondia a uma pedrinha que era armazenada em um saco.
No caso das pedrinhas, cada animal que saía para o pasto de manhã correspondia a uma pedra que era guardada em um saco de couro. No final do dia, quando os animais voltavam do pasto, era feita a correspondência inversa, onde, para cada animal que retornava, era retirada uma pedra do saco. Se no final do dia sobrasse alguma pedra, é porque faltava algum dos animais e se algum fosse acrescentado ao rebanho, era só acrescentar mais uma pedra.
Conforme Imenes(1999), além de pedrinhas, o homem usou outros recursos para auxiliá-lo nas contagens.
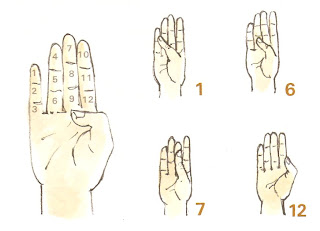
 O próprio corpo teve um papel importantíssimo ao longo dos milhares de anos que se levou para criar os números.
O próprio corpo teve um papel importantíssimo ao longo dos milhares de anos que se levou para criar os números. De diferentes maneiras, as mãos eram utilizadas para realizar contagens.
Origem do sistema de numeração indo-arábico
A origem do nosso sistema de numeração indo-arábico é bastante antiga. Ele surgiu, conforme http://www.iejusa.org.br/cienciaetecnologia?matematica.php, na Ásia, há muitos séculos, no vale do rio Indo, onde hoje é o Paquistão.
Foram as civilizações que floresceram após 1 500 a.C. nessa região do vale do rio Indo que desenvolveram um sistema de numeração que serviu de base para o nosso. Esse sistema era não-posicional, ou seja, colocado um dos símbolos à direita ou à esquerda de um outro, o valor dos números assim obtidos não se altera.
Foram as civilizações que floresceram após 1 500 a.C. nessa região do vale do rio Indo que desenvolveram um sistema de numeração que serviu de base para o nosso. Esse sistema era não-posicional, ou seja, colocado um dos símbolos à direita ou à esquerda de um outro, o valor dos números assim obtidos não se altera.

Até que fosse desenvolvida a numeração decimal posicional, ainda se passariam alguns séculos. Parece que o sistema de numeração posicional indiano se configurou apenas por volta do século V, mas ara a criação desse sistema decimal posicional os indianos receberam influências de muitos dos povos com os quais tiveram contato. O princípio posicional já aparecia no sistema dos mesopotâmicos. A base dez era usada pelos egípcios e chineses. Quanto ao zero, existem indícios de que já era usado pelos mesopotâmicos na fase final de sua civilização.
 O grande mérito dos indianos foi o de reunir essas diferentes características num mesmo sistema numérico
O grande mérito dos indianos foi o de reunir essas diferentes características num mesmo sistema numérico
Por que o sistema se chama indo-arábico?

Aos árabes é creditada a difusão do sistema indiano. Circunstâncias especiais favoreceram esse fato.
Até por volta do século VI , a Arábia era habitada principalmente por tribos nômades do deserto. Nessa época, poucas cidades funcionavam como centros de comércio. No século VII, teve início a religião islâmica, fundada por Maomé, que conseguiu unir as tribos do deserto.
Os seguidores de Maomé, invadindo numerosos territórios vizinhos, passaram a controlar, em pouco mais de um século, um imenso império, que se estendia da Espanha ao vale do rio Indo.
No contato com os indianos, os árabes assimilaram o sistema de numeração decimal posicional. Ao invadirem a Europa, por volta do século VIII, para lá levaram essa representação dos números.
Por terem os árabes, dessa forma, difundido o sistema numérico indiano, ele passou a ser conhecido como indo-arábico.
Como antes da invenção da imprensa, no século XV, os livros eram copiados manualmente, um a um e cada copista tinha a sua caligrafia, as letras e os símbolos para representar números foram sofrendo muitas modificações durante todos esses séculos de copiagem manual.
Fonte: http://www.iejusa.org.br/cienciaetecnologia/matematica.php
Até por volta do século VI , a Arábia era habitada principalmente por tribos nômades do deserto. Nessa época, poucas cidades funcionavam como centros de comércio. No século VII, teve início a religião islâmica, fundada por Maomé, que conseguiu unir as tribos do deserto.
Os seguidores de Maomé, invadindo numerosos territórios vizinhos, passaram a controlar, em pouco mais de um século, um imenso império, que se estendia da Espanha ao vale do rio Indo.
No contato com os indianos, os árabes assimilaram o sistema de numeração decimal posicional. Ao invadirem a Europa, por volta do século VIII, para lá levaram essa representação dos números.
Por terem os árabes, dessa forma, difundido o sistema numérico indiano, ele passou a ser conhecido como indo-arábico.
Como antes da invenção da imprensa, no século XV, os livros eram copiados manualmente, um a um e cada copista tinha a sua caligrafia, as letras e os símbolos para representar números foram sofrendo muitas modificações durante todos esses séculos de copiagem manual.
Fonte: http://www.iejusa.org.br/cienciaetecnologia/matematica.php
Alterações na escrita dos dez algarismos da numeração indo-arábica
Como o sistema de numeração criado na Índia foi adotado pelos árabes e passado aos europeus, é natural que a forma de escrever os dez algarismos fosse sofrendo alterações.
 Entre os árabes, os símbolos acabaram por tomar a seguinte configuração, que é por eles utilizada atualmente:
Entre os árabes, os símbolos acabaram por tomar a seguinte configuração, que é por eles utilizada atualmente:  Na Índia, os símbolos também continuaram a se modificar. Uma das formas hoje ali utilizadas é esta:
Na Índia, os símbolos também continuaram a se modificar. Uma das formas hoje ali utilizadas é esta:
 E quanto a nós, hoje em dia, representamos os dez algarismos assim:
E quanto a nós, hoje em dia, representamos os dez algarismos assim:
 Fonte: http://www.iejusa.org.br/cienciaetecnologia/matematica.php
Fonte: http://www.iejusa.org.br/cienciaetecnologia/matematica.php
 Entre os árabes, os símbolos acabaram por tomar a seguinte configuração, que é por eles utilizada atualmente:
Entre os árabes, os símbolos acabaram por tomar a seguinte configuração, que é por eles utilizada atualmente:  Na Índia, os símbolos também continuaram a se modificar. Uma das formas hoje ali utilizadas é esta:
Na Índia, os símbolos também continuaram a se modificar. Uma das formas hoje ali utilizadas é esta: E quanto a nós, hoje em dia, representamos os dez algarismos assim:
E quanto a nós, hoje em dia, representamos os dez algarismos assim: Fonte: http://www.iejusa.org.br/cienciaetecnologia/matematica.php
Fonte: http://www.iejusa.org.br/cienciaetecnologia/matematica.php
Numeração Egípcia
Os egípcios escreviam os números usando esses sinais:
 O sistema numérico egípcio é decimal, ou seja, ele tem base dez.
O sistema numérico egípcio é decimal, ou seja, ele tem base dez.
Fonte: IMENES, Luiz Márcio. Vivendo a Matemática: os números na história da civilização. São Paulo: scipione,1999.
 O sistema numérico egípcio é decimal, ou seja, ele tem base dez.
O sistema numérico egípcio é decimal, ou seja, ele tem base dez.Fonte: IMENES, Luiz Márcio. Vivendo a Matemática: os números na história da civilização. São Paulo: scipione,1999.
Sistema de Numeração da Mesopotâmia
A Numeração na Grécia Antiga
Os gregos usavam as vinte e quatro letras de seu alfabeto acrescidas de três outros sinais para representar os números:
 Para representar os múltiplos de mil, até nove mil, eles usavam novamente as primeiras letras do alfabeto acompanhadas de um pequeno risco:
Para representar os múltiplos de mil, até nove mil, eles usavam novamente as primeiras letras do alfabeto acompanhadas de um pequeno risco:
A contagem era feita por grupos de dez.
Fonte: IMENES, Luiz Márcio. Vivendo a Matemática: os números na história da civilização. São Paulo: scipione,1999.
O Sistema Numérico Romano
Trata-se de um sistema de base dez, em que comparecem novos símbolos para o cinco, o cinqüenta e o quinhentos. O que facilita a escrita de alguns números.

Fonte: IMENES, Luiz Márcio. Vivendo a Matemática: os números na história da civilização. São Paulo: scipione,1999.

Fonte: IMENES, Luiz Márcio. Vivendo a Matemática: os números na história da civilização. São Paulo: scipione,1999.
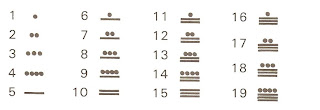
O Sistema de Numeração dos Maias
Esses são os números maias de um a dezenove:
 O vinte era registrado da seguinte maneira:
O vinte era registrado da seguinte maneira:
 O vinte era registrado da seguinte maneira:
O vinte era registrado da seguinte maneira:  O zero era um símbolo que lembra uma concha:
O zero era um símbolo que lembra uma concha: A contagem é feita em grupos de vinte, o que faz supor que a base do sistema maia era vinte. Entretanto, a partir do número trezentos e sessenta, as regras do sistema se complicam e os agrupamentos deixam de ser feitos de vinte em vinte.
A contagem é feita em grupos de vinte, o que faz supor que a base do sistema maia era vinte. Entretanto, a partir do número trezentos e sessenta, as regras do sistema se complicam e os agrupamentos deixam de ser feitos de vinte em vinte.Fonte: IMENES, Luiz Márcio. Vivendo a Matemática: os números na história da civilização. São Paulo: scipione,1999.
A Origem da palavra CÁLCULO
No pastoreio, o pastor usava várias formas para controlar o seu rebanho, conforme http://pessoal.sercomtel.com.br/matematica/fundam/numeros/numeros.htm#m10101 . Pela manhã, ele soltava os seus carneiros e analisava ao final da tarde, se algum tinha sido roubado, fugido, se perdido do rebanho ou se havia sido acrescentado um novo carneiro ao rebanho. Assim eles tinham a correspondência um a um, onde cada carneiro correspondia a uma pedrinha que era armazenada em um saco.
No caso das pedrinhas, cada animal que saía para o pasto de manhã correspondia a uma pedra que era guardada em um saco de couro. No final do dia, quando os animais voltavam do pasto, era feita a correspondência inversa, onde, para cada animal que retornava, era retirada uma pedra do saco. Se no final do dia sobrasse alguma pedra, é porque faltava algum dos animais e se algum fosse acrescentado ao rebanho, era só acrescentar mais uma pedra. A palavra que usamos hoje, cálculo, é derivada da palavra latina calculus, que significa pedrinha.
No caso das pedrinhas, cada animal que saía para o pasto de manhã correspondia a uma pedra que era guardada em um saco de couro. No final do dia, quando os animais voltavam do pasto, era feita a correspondência inversa, onde, para cada animal que retornava, era retirada uma pedra do saco. Se no final do dia sobrasse alguma pedra, é porque faltava algum dos animais e se algum fosse acrescentado ao rebanho, era só acrescentar mais uma pedra. A palavra que usamos hoje, cálculo, é derivada da palavra latina calculus, que significa pedrinha.
A palavra DÍGITO
A palavra dígito, sinônima de ‘algarismo’, provém de digitus, que em latim significa ‘dedo’.

Fonte: IMENES, Luiz Márcio. Vivendo a Matemática: os números na história da civilização. São Paulo: scipione,1999.

Fonte: IMENES, Luiz Márcio. Vivendo a Matemática: os números na história da civilização. São Paulo: scipione,1999.
Curiosidade:Números amigáveis e número mágico
Os números possuem inimagináveis curiosidades. Dentre elas algumas que são encontradas no site www.somatematica.com.br são:
Números amigáveis --> pares de números onde um deles é a soma dos divisores do outro. Como exemplo, os divisores de 220 são: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110 cuja soma é 284. Por outro lado, os divisores de 284 são: 1, 2, 4, 71 e 142 e a soma deles é 220. Fermat descobriu também o par 17.296 e 18.416. Descartes descobriu o par 9.363.584 e 9.437.056.
Número mágico --> é o número 1089 porque se você escolher qualquer número de três algarismos distintos, por exemplo, 875, e depois escrever este número de trás para frente e subtrair o menor do maior: 875 - 578 = 297. Após inverter também esse resultado e fazer a soma: 297 + 792 = 1089, você obterá o número mágico.
quinta-feira, 21 de agosto de 2008
Curiosidade: Números pares e ímpares
Lá pelos 1000 anos a.C., os chineses representaram os números combinando círculos brancos e círculos pretos. Os brancos representavam números ímpares e os pretos, números pares.
Tais métodos também encontram entre os gregos, principalmente os Pitagóricos (discípulos de Pitágoras). Estes chamavam os números pares de “fêmeas”, e os ímpares de “machos” (com exceção do 1). O número 1 não era um número, mas o elemento formador de todos os outros números.
É interessante dentro da concepção dos números ímpares como sendo números machos, a dos números “afeminados”. Todo número ímpar que não fosse primo era considerado “afeminado”, como por exemplo, os números 9, 15, 25, etc. A razão disso se achava na representação por meio de círculos. O número cinco, por exemplo, não era “afeminado”, pois podia ser obtido do “casamento” de um macho com uma fêmea, conservando-se a posição pré-estabelecida dos círculos. Já o nove não podia ser obtido de um “casamento” perfeito entre macho e fêmea.
Não se podia dizer que o nove resultava do casamento do 3 (macho) com o 6 (fêmea), pois não representava o três, embora os círculos representassem o 6. 4 Aliás, o 5 representava o primeiro “casamento” perfeito, por isso o 5 representava o “matrimônio”. O seis por sua vez era o frio. Existiam os números perfeitos, cujos fatores inteiros, somados, reproduziam o próprio número, como no caso do 6, pois seus fatores 1, 2, 3, somados 1 + 2 + 3 = 6, ou o 28 = 1 + 2 + 4 + 7 + 14.
Fonte: http://www.colegiomarcopolo.com.br/Mat/ComoSurgiram.pdf
Tais métodos também encontram entre os gregos, principalmente os Pitagóricos (discípulos de Pitágoras). Estes chamavam os números pares de “fêmeas”, e os ímpares de “machos” (com exceção do 1). O número 1 não era um número, mas o elemento formador de todos os outros números.
É interessante dentro da concepção dos números ímpares como sendo números machos, a dos números “afeminados”. Todo número ímpar que não fosse primo era considerado “afeminado”, como por exemplo, os números 9, 15, 25, etc. A razão disso se achava na representação por meio de círculos. O número cinco, por exemplo, não era “afeminado”, pois podia ser obtido do “casamento” de um macho com uma fêmea, conservando-se a posição pré-estabelecida dos círculos. Já o nove não podia ser obtido de um “casamento” perfeito entre macho e fêmea.
Não se podia dizer que o nove resultava do casamento do 3 (macho) com o 6 (fêmea), pois não representava o três, embora os círculos representassem o 6. 4 Aliás, o 5 representava o primeiro “casamento” perfeito, por isso o 5 representava o “matrimônio”. O seis por sua vez era o frio. Existiam os números perfeitos, cujos fatores inteiros, somados, reproduziam o próprio número, como no caso do 6, pois seus fatores 1, 2, 3, somados 1 + 2 + 3 = 6, ou o 28 = 1 + 2 + 4 + 7 + 14.
Fonte: http://www.colegiomarcopolo.com.br/Mat/ComoSurgiram.pdf
Assinar:
Comentários (Atom)



